5. Perkalian Vektor dan Skalar
Sebelum kita belajar mengenai
perkalian vektor, terlebih dahulu kita berkenalan dengan vektor-vektor satuan.
Vektor satuan (unit vektor) merupakan suatu vektor yang besarnya = 1. vektor satuan tidak mempunyai satuan. Vektor satuan berfungsi untuk menunjukan suatu arah dalam ruang. Untuk membedakan vektor satuan dari vektor biasa maka vektor satuan dicetak tebal (untuk tulisan cetak) atau di atas vektor satuan disisipkan tanda ^ (untuk tulisan tangan)
Pada sistem koordinat kartesius (xyz) kita menggunakan vektor satuan i untuk menunjukkan arah sumbu x positif, vektor satuan j untuk menunjukkan arah sumbu y positif, vektor satuan k untuk menunjukkan arah sumbu y positif.
Untuk memudahkan pemahaman dirimu, perhatikan contoh berikut ini. Misalnya terdapat sebuah vektor F sebagaimana tampak pada gambar di bawah.
Pada gambar di atas, tampak bahwa vektor satuan i menunjukkan arah sumbu x positif dan vektor satuan j menunjukkan arah sumbu y positif. Kita dapat menyatakan hubungan antara vektor komponen dan komponenya masing-masing, sebagai berikut :
Fx = Fxi
Fy = Fyj
Kita dapat menulis vektor F dalam komponen-komponennya sebagai berikut :
F = Fxi + Fyj
Misalnya terdapat dua vektor, A dan B pada sistem koordinat xy, di mana kedua vektor ini dinyatakan dalam komponen-komponennya, sebagaimana tampak di bawah :
A = Axi + Ayj
B = Bxi + Byj
Bagaimana jika A dan B dijumlahkan ? gampang…
R = A + B
R = (Axi + Ayj) + (Bxi + Byj)
R = (Ax + Bx)i + (Ay + By)j
R = Rxi + Ryj
Apabila tidak semua vektor berada pada bidang xy maka kita bisa menambahkan vektor satuan k, yang menunjukkan arah sumbu z positif.
A = Axi + Ayj + Azk
B = Bxi + Byj + Bzk
Jika vektor A dan B dijumlahkan maka akan diperoleh hasil sebagai berikut :
R = A + B
R = (Axi + Ayj + Azk) + (Bxi + Byj + Bzk)
R = (Ax + Bx)i + (Ay + By)j + (Az + Bz)k
R = Rxi + Ryj + Rzk
Perkalian titik menggunakan komponen vektor satuan
Kita dapat menghitung
perkalian skalar secara langsung jika kita mengetahui komponen x, y dan z dari vektor
A dan
B (vektor yang diketahui).
Untuk melakukan perkalian titik dengan cara ini, terlebih dahulu kita lakukan perkalian titik dari vektor satuan, setelah itu kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
Vektor satuaj i, j dan k saling tegak lurus satu sama lain, sehingga memudahkan kita dalam perhitungan. Menggunakan persamaan perkalian skalar yang telah diturunkan di atas (A.B = AB cos teta) kita peroleh :
i . i = j . j = k . k = (1)(1) cos 0 = 1
i . j = i . k = j . k = (1)(1) cos 90o = 0
Sekarang kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
A . B = Axi . Bxi + Axi . Byj + Axi . Bzk +
Ayj . Bxi + Ayj . Byj + Ayj . Bzk +
Azk . Bxi + Azk . Byj + Azk . Bzk
A . B = AxBx (i . i) + AxBy (i . j) + Ax Bz (i . k) +
AyBx (j . i) + AyBy (j . j) + AyBz (j . k) +
AzBx (k . i) + AzBy (k . j) + AzBz (k . k)
Bahasa apa’an neh… dipahami perlahan-lahan ya….
Karena i . i = j . j = k . k = 1 dan i . j = i . k = j . k = 0, maka :
A . B = AxBx (1) + AxBy (0) + Ax Bz (0) +
AyBx (0) + AyBy (1) + AyBz (0) +
AzBx (0) + AzBy (0) + AzBz (1)
A . B = AxBx (1) + 0 + 0 +
0 + AyBy (1) + 0 +
0 + 0 + AzBz (1)
A . B = AxBx + AyBy + AzBz
Berdasarkan hasil perhitungan ini, bisa disimpulkan bahwa perkalian skalar atau perkalian titik dari dua vektor adalah jumlah dari perkalian komponen-komponennya yang sejenis.
Gampang khan ? dipahami perlahan-lahan… ntar juga ngerti kok… kaya belajar naek sepeda agar dirimu semakin memahami bahasa alien di atas, mari kita kerjakan latihan soal di bawah ini
Contoh Soal 1 :
Besar vektor A dan B berturut-turut adalah 5 dan 4, sebagaimana tampak pada gambar di bawah. Sudut yang terbentuk adalah 90o. Hitunglah perkalian titik kedua vektor tersebut…
Panduan jawaban :
Sebelum kita menghitung perkalian titik vektor A dan B, terlebih dahulu kita ketahui komponen vektor kedua tersebut.
Ax = (5) cos 0o = (5) (1) = 5
Ay = (5) sin 0o = (5) (0) = 0
Az = 0
Bx = (4) cos 90o = (4) (0) = 0
By = (4) sin 90o = (4) (1) = 1
Bz = 0
Vektor A hanya mempunyai komponen vektor pada sumbu x dan vektor B hanya mempunyai komponen vektor pada sumbu y. Komponen z bernilai nol karena vektor A dan B berada pada bidang xy.
Sekarang kita hitung perkalian titik antara vektor A dan B menggunakan persamaan perkalian titik dengan vektor komponen :
A . B = Ax Bx + AyBy + AzBz
A . B = (5) (0) + (0) (1) + 0
A . B = 0 + 0 + 0
A . B = 0
Masa sich hasilnya nol ?
Coba kita bandingkan dengan cara pertama
A.B = AB cos teta
A.B = (4)(5) cos 90
A.B = (4) (5) (0)
A.B = 0
Hasilnya sama.
Contoh Soal 2 :
Besar vektor A dan B berturut-turut adalah 5 dan 4, sebagaimana tampak pada gambar di bawah. Hitunglah perkalian titik kedua vektor tersebut, jika sudut yang terbentuk adalah 30o
Panduan jawaban :
Sebelum kita menghitung perkalian titik vektor A dan B, terlebih dahulu kita ketahui komponen vektor kedua tersebut.
Komponen z bernilai nol karena vektor A dan B berada pada bidang xy.
Sekarang kita hitung perkalian titik antara vektor A dan B menggunakan persamaan perkalian titik dengan vektor komponen :
Coba kita bandingkan dengan cara pertama.
Hasilnya sama.
Perkalian silang menggunakan komponen vektor satuan
Kita dapat menghitung perkalian silang secara langsung jika kita mengetahui komponen vektor yang diketahui. Urutannya sama dengan perkalian titik.
Pertama-tama, kita lakukan perkalian antara vektor-vektor satuan i, j dan k. Hasil perkalian vektor antara vektor satuan yang sama adalah nol.
i x i = j x j = k x k = 0
Dengan berpedoman pada persamaan perkalian vektor yang telah diturunkan sebelumnya (A x B = AB sin teta) dan sifat anti komutatif dari perkalian vektor (A x B = – B x A), maka kita peroleh :
i x j = -j x i = k
j x k = -k x j = i
k x i = -i x k = j
Sekarang kita nyatakan vektor A dan B dalam komponen-komponennya, menguraikan perkaliannya dan menggunakan perkalian dari vektor-vektor satuannya.
A x B = (Axi + Ayj + Azk) x (Bxi + Byj + Bzk)
A x B = Axi x Bxi + Axi x Byj + Axi x Bzk +
Ayj x Bxi + Ayj x Byj + Ayj x Bzk +
Azk x Bxi + Azk x Byj + Azk x Bzk
A x B = AxBx (i x i) + AxBy (i x j) + Ax Bz (i x k) +
AyBx (j x i) + AyBy (j x j) + AyBz (j x k) +
AzBx (k x i) + AzBy (k x j) + AzBz (k x k)
Karena i x i = j x j = k x k = 0 dan i x j = -j x i = k, j x k = -k x j = i, k x i = -i x k = j, maka :
A x B = AxBx (0) + AxBy (k) + Ax Bz (-j) +
AyBx (-k) + AyBy (0) + AyBz (i) +
AzBx (j) + AzBy (-i) + AzBz (0)
A x B = AxBy (k) + Ax Bz (-j) +
AyBx (-k) + AyBz (i) +
AzBx (j) + AzBy (-i)
A x B = AxBy (k) + Ax Bz (-j) + AyBx (-k) + AyBz (i) + AzBx (j) + AzBy (-i)
A x B = (AyBz - AzBy)i + (AzBx - Ax Bz)j + (AxBy - AyBx )k
Pahami perlahan-lahan….
Jika C = A x B maka komponen-komponen dari C adalah sebagai berikut :
Cx = AyBz - AzBy
Cy = AzBx - Ax Bz
Cz = AxBy - AyBx
























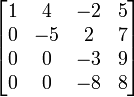

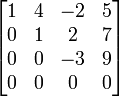



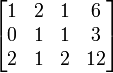 Baris ke 2 dikurangi baris ke 1
Baris ke 2 dikurangi baris ke 1 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1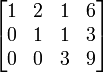 Baris ke 3 ditambah 3 kali baris ke 2
Baris ke 3 ditambah 3 kali baris ke 2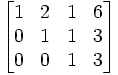 Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)
Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris)
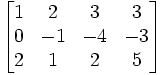 Baris ke 2 dikurangi 2 kali baris ke 1
Baris ke 2 dikurangi 2 kali baris ke 1 Baris ke 3 dikurangi 2 kali baris ke 1
Baris ke 3 dikurangi 2 kali baris ke 1 Baris ke 3 dikurangi 3 kali baris ke 2
Baris ke 3 dikurangi 3 kali baris ke 2 Baris ke 3 dibagi 8 dan baris ke 2 dibagi -1
Baris ke 3 dibagi 8 dan baris ke 2 dibagi -1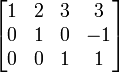 Baris ke 2 dikurangi 4 kali baris ke 3
Baris ke 2 dikurangi 4 kali baris ke 3 Baris ke 1 dikurangi 3 kali baris ke 3
Baris ke 1 dikurangi 3 kali baris ke 3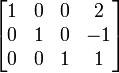 Baris ke 1 dikurangi 2 kali baris ke 2 (Matriks menjadi Eselon-baris tereduksi)
Baris ke 1 dikurangi 2 kali baris ke 2 (Matriks menjadi Eselon-baris tereduksi)
![[equation9.png]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhO0gLv4m3ZMQcS4P_Zx0XWQhurgEdXd4Uhs4w36-ItCsj1CrhNNgSn_ieqV2_4LF7GjVY2pfjfTIMbtm7xQ6hZqTZAHMfElJ6B_oU6n8lUUJ6XVn1YFXgoZiaA_W8juQ-z5bkwPresL8F0/s1600/equation9.png)